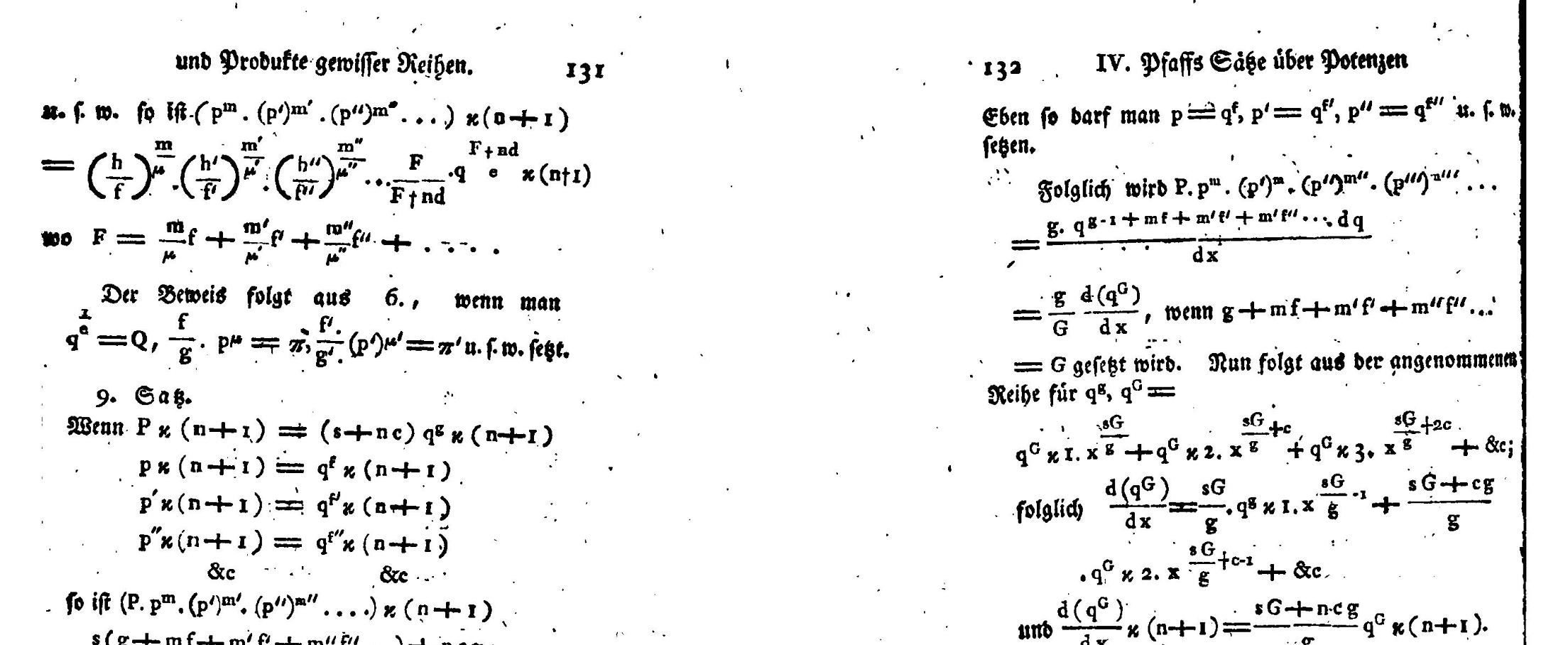“It is the greatest remedy for the mind if a few thoughts can be found from which infinite others arise in order, just as from the assumption of a few numbers, from one to ten, all the other numbers can be derived in order.”
—Leibniz, ‘Of an Organum or Ars Magna of Thinking’
At the twilight of the 18th century, European mathematics was still recovering from the monumental revelations of the 17th century in its discovery of the calculus. The veritable moral panic provoked by the success of infinite series methods showed no signs of abating. Before Cauchy would go on to provide his rigorous formalisation of the calculus by grounding it in the theory of continuous functions, the question of the foundations of analysis was up in the air. In this state of epistemological suspension a variety of different directions were pursued. One of these directions, following on from the mathematical work of Euler in his Introductio in analysin infinitorum of 1748, and championing the philosophical ideal of Gottfried Wilhelm Leibniz in his search for a characteristica universalis, was that of Carl Friedrich Hindenburg and his combinatorial school.
From Euler’s work stemmed the notion of treating functions as objects to be manipulated algebraically with the aid of infinite series and continuous fractions. Lagrange in his Théorie des fonctions analytiques (1797) had based the differential and integral calculus on a power series approach. The combinatorialists took a novel approach in algebraic analysis that was called the Analysis des Endlichen, or finite analysis, seeking a uniquely algebraic basis for the infinitesimal calculus. They expropriated Euler’s use of the infinite series and attempted to use this as the basis upon which to construct the entire mathematical edifice. The motivation was to develop a general science of the structure of formulae utilising combinatorial analysis. There was a focus on developing new forms of notation, some of which were particularly unwieldy and indeed ugly (Cajori 1993, 443-445), and a pioneering employment of tabular methods for the representation of combinatorial aggregates. The school were the first in setting up principles for working with tables of permutations, combinations, and variations in order to prevent the introduction of errors.
Of prime importance for this project was the polynomial formula, for which a few proofs had recently been attempted. Hindenburg gave a proof for the general polynomial formula (Hindenburg 1779), or, as it was called at the time, “die Potenzierung des Infinitinoms”. Unlike previous attempts, Hindenburg’s formulation had the merit of allowing for a generalisation for fractional and negative exponents.
It was an extremely important result for working with power series because division, exponentiation and extraction of roots could be reworked into this form by taking the respective negative, natural, and fractional powers. Because of this Klügel, one of Hindenburg’s followers, described the polynomial formula as the “pinnacle from which one can survey the region of analysis”.
Another member of the school, Heinrich August Rothe showed that the solution of arbitrary or transcendental equations could be found by applying the polynomial formula to obtain what is called series reversion. Lagrange had already displayed the principles of this technique in what is now called the Lagrange inversion theorem, but he was more concerned with its application to astronomical phenomena. Rothe provided the more generalised solution. The filled the rest of the school will great excitement because it demonstrated the efficacy of the polynomial formula in general algebraic solutions, supplying much needed proof of work for their methodical engine.
In Leibniz, to whom multiple references are made in Hindenburg’s work (Hindenburg 1796), the school found its conceptual drive. Inheriting the spirit of the ars combinatoria or “art of combining” from Renaissance figures such as Ramon Llull and Athanasius Kircher, Leibniz dreamt of a symbolic system that would produce complex conceptual aggregates from the rule-governed combination of simpler ones. The ars combinatoria would then become an ars inveniendi, an art of invention or discovery. In his Dissertatio de arte combinatoria (1666), written at Leipzig University, where Hindenburg would later become professor of physics, Leibniz outlines a schematic for such a system. Though an early work, which is more prospective than methodological, the theme would haunt his later writings, insinuating itself constantly as a kind of peradam or philosophical stone. Later, Gödel would go so far as to suggest that this pursuit fed directly into his work on the calculus. In ‘Of Universal Synthesis and Analysis’, Leibniz writes
The art of combinations in particular is, in my opinion, the science which treats of the forms of things or of formulae in general (it could also be called generally the science of symbols, or of forms. That is, it is the science of quality in general, or, of the like and the unlike … It is distinguished from algebra, which is concerned with formulae applied to quantity, i.e. with the equal and the unequal. Consequently, algebra is subordinate to the art of the combinations, and constantly uses its rules.
It is the final statement here that is key. The school saw combinatorics as a global method that would subsume algebra as a local subdiscipline. For them, combinatorial theory could serve as the basis for pure mathematics and tackle its critical questions. This ambition for combinatorics naturally seems somewhat absurd today. Philippe Seguin links this to the post-Kantian spirit of the age (Seguin 2005). Since we are talking about the climate in which Fichte had sought to root the science of consciousness in the axiom $A = A$, it seems only natural that Hindenburg, not himself a considerable mathematician, would seek to ground all of algebra on the multinomial formula. There was, apparently, a tendency towards the universalisation of quite particular results. Either way, the general mood was to rid analysis of geometry and so called “intuition”, as a reaction against Kant’s attempt to ground mathematics in the formal intuitions of time and space. The return to the rationalist Leibniz makes sense in this light. Adopting a different perspective, if we consider the manner in which mathematics would continue to develop with the introduction of the limit concept and the expansion of the role of imaginary numbers, the school may even have been prescient in the move towards symbolic abstraction and away from geometric intuition.
As a method of mathematical education, the ways of the combinatorial school lived on in Germany for much longer into the 18th century (Jahnke 1993). In some ways, despite the labyrinthine complexity of the notation when it came to Hindenburg’s proofs, the focus on series was a good means of illustrating the application of elementary mathematical methods at varied degrees of abstraction. As Jahnke has it, it formed a part of the Denkwelt or ‘cognitive universe’ of German mathematical Bildung during the period, long after the school fell out of favour.
Although they yielded some concrete results, as described above, and must be included in any exhaustive history of the development of modern mathematics, the combinatorial school are a strong candidate for the most reviled movement in the standard reference works. In a subchapter entitled “Ridiculous Interlude” (!), E. T. Bell writes that
The combinatorial school headed by C.F. Hindenburg (1741-1808), was the unlovely offspring of two human failings, neither of which is popularly supposed to have any relevance for the sublimities of pure mathematics: blind hero worship and national jealousy. (Bell 1945, 290)
While Bell is correct in locating the ultimate failure of the school in its dogmatic philosophical foundations, he is of course writing in a period shortly before the re-emergence of combinatorics as a dignified discipline in its own right thanks the age of computation and the subsequent vindication of discrete mathematics. As for “blind hero worship”, there seems to be little documentary evidence to support any character assertions about Hindenburg besides his prodigious capacity as an organiser of scholars and journals. There is equally something fishy about the attribution of national jealousy here. It is certain that German mathematics suffered a drought of international superstars in the 18th century, and it would not be until the ascent of Gauss at the dawn of 19th century that the country would find itself on an equal footing with France and England again. However, this trend towards sensationalising personality cults and national rivalries, a hallmark of the Newton-Leibniz literature, is always extremely speculative and never particularly useful.
Elsewhere, Cajori, in his characterisation of the period’s experimentation with infinite series, notes that
Euler reached some very pretty results on infinite series, now well known, and also some very absurd results, now quite forgotten. The faults of his time found their culmination in the Combinatorial School in Germany, which has now passed into deserved oblivion. (Cajori, 1909, 390).
This seems like far too summary a dismissal since Hindenburg, Rothe, and Kramm’s results are still used today. In the Art of Computer Programming 4A, Donald Knuth writes of “Hindenburg’s hype”, insisting that his “small successes led him to believe that he had made revolutionary advances in mathematics—although he did condescend to remark that other people such as de Moivre, Euler, and Lambert had come close to making similar discoveries” (Knuth 1997, 507-508). There is something suspicious about this disavowal which seems like a cribbing of the previous histories, because elsewhere in the tome Knuth cites no less than three of Hindenburg’s works and one of Rothe’s. A vindication of certain of the school’s methods in the light of the significance of combinatorial methods for computer science is perhaps overdue. This roster of comments is worth clipping and comparing, for there is an implacably widespread hostility shown towards Hindenburg and his followers amongst historians of mathematics.
Hindenburg’s influence fared rather better in philosophy. Due to his fervid admiration for Leibniz, this is perhaps fitting. For example, in Salomon Maimon’s Schlußanmerkung, Maimon addresses the controversy that had had arisen between Hindenburg and Wenceslav Johann Gustav Karstens over the former’s treatment of Euclidean parallels with some interest (Freudenthal 2006, 106). It is equally certain that the bizarre mathematical mystic Józef Maria Hoene-Wroński, another enemy of the rather argumentative Bell, was familiar with the methods of the combinatorial school. However, it is in the work of Novalis, who almost certainly studied under him at Leipzig, that Hindenburg’s presence is felt most keenly. We know for certain that Novalis owned Hindenburg’s books, as well as those of other members of the school. In his Allegemeine Brouillon, his project for a Romantic encylopaedia, Novalis cites Hindenburg a number of times and posits combinatorial analysis as a model of conceptual synthesis in general. In Fragment 547, entitled ‘Musical Mathematics’, we find the following:
Combinatorial analysis leads to numerical imaginings—and teaches the art of the composition of numbers—mathematical basso continuo. (Pythagoras. Leibniz). Language is a musical instrument of ideas. The poet, rhetorician and philosopher play and compose grammatically. A fugue is thoroughly logical or scientific—It may also be treated poetically.
Basso continuo includes musical algebra and analysis. Combinatorial analysis is critical algebra and analysis—and the theory of musical composition stands in the same relation to basso continuo, as combinatorial analysis does to simple analysis.
Many mathematical problems cannot be solved in isolation, but only in combination with other problems—from a higher point of view—simply through a combinatorial operation. (Novalis, 2007, 96-97)
It is this project for a Romantic encyclopaedia that captures the philosophical direction of the combinatorial school most vividly. In fact, Novalis’ formula for Romanticisation was that of raising the object of enquiry to a higher power, Potenzierung: a clear nod to the school’s methods. In Novalis’ dream of a coalition system between the arts and sciences we see something of the school’s extreme ambitions regarding the foundations of mathematics. During what is a clear restatement of Hindenburg’s intent with the multinomial, Novalis remarks that “science on the whole is generally the total function of the data and the facts—the n-th power of the binomial series of the data and the facts” (Novalis, 2007, 30). At the suggestion that all the world’s knowledge could be contained within a power series expansion, we truly find ourselves in the outer reaches of philosophical speculation.
The proto-foundationalist project of the combinatorial school was a failure. In this, their dogmatic Leibnizianism was a dead end. However, there was truly something of the spirit of composition found in contemporary pure mathematics in their grasping for the infinite via the combination and modulation of discrete elements, in their attempts to raise so-called finite analysis to a series of higher powers. It is this spirit that is undeserving of the layers of snark and disdain that Hindenburg and his peers have accrued with the passage of time. It is here that methodical conceptual reanimation can provide some due dignity.
Bibilography
BELL, E. T.
1945, The Development of Mathematics. McGraw-Hill Book Company: London.
CAJORI, FLORIAN
1909, A History of Mathematics, Macmillan & Co.: London.
1993, A History of Mathematical Notations, Dover: New York.
EULER, LEONHARD
1748, Introducio ad analysin infinitorum
FREUDENTHAL
2006, Definition and Construction: Salomon Maimon’s Philosophy of Geometry, Max Planck Insitute for the History of Science.
HINDENBURG, CARL FRIEDRICH
1778, Methodus nova et facilis serierum infinitarum exhibendi dignitates exponentis indeterminati […], Göttingen
1779, Infinitomii dignitatum exponentis indeterminate historia leges ae formulae […], Göttingen.
1781, Novi systemais permutationum combinationum ae variationum primas lineas […], Leipzig.
1781-85, Leipziger Magazin für Naturkunde, Mathematik und Astronomie, Leipzig.
1786-88, Leipziger Magzin für reine und angewandte Mathematik, Leipzig.
1795-1800, Archiv für reine und angewandte Mathematik, Leipzig.
1796-1803, Sammlung kombinatorisch-analytischer Abhandlungen. Leipzig.
JAHNKE, HANS NIEL
1993, ‘Algebraic Analysis in Germany, 1780-1840’, Historia Mathematica 20, 265-284.
KNUTH, DONALD
1997, Art of Computer Programming 4A: Combinatorial Algorithms, Addison-Wesley: Boston.
LAGRANGE, JOSEPH LOUIS
1797, Théorie des fonctions analytiques. Paris. Oeuvres, 9.
LEIBNIZ, GOTTFRIED WILHELM
1973, Philosophical Writings, Everyman: London.
ROTHE, H. A.
1793, Formulae de serierum reversione demonstratio universalis signis localibus combinatorio-analyticorum vicariis exhibita. Leipzig.
NOVALIS
2007, Notes for a Romantic Encyclopaedia, State University of New York Press: New York.
SEGUIN, PHILIPPE
2005, ‘Le recherche d’un fondement absolu des mathématiques par L’Ecole combinatoire de C. F. Hindenburg (1741-1808)’, Philisophia Scientiae, CS 5